Mesure de position et mesure de dispersion
Nicolas Chauvel Commission Recherche SFMU 2015
En recherche quantitative, la statistique est omniprésente. Nous nous intéresserons ici uniquement à sa dimension descriptive. Nous allons définir les principaux paramètres statistiques à notre disposition pour décrire la distribution d'une variable quantitative (comme par exemple l'âge) au sein d'une population. Il existe des mesures de position (moyenne et médiane) qui estiment la tendance centrale (« centre de gravité ») d'une population, et des mesures de dispersion (ecart-type et intervalle interquartile notamment) qui estiment son étalement.
Mesures de position [1]
Moyenne
Au sein d'un échantillon, elle correspond à la somme des valeurs prise par la variable, divisée par le nombre de ces valeurs. Elle est une bonne mesure de la tendance centrale pour les distributions symétriques ou grossièrement symétriques. Mais elle peut être biaisée dans le cas contraire. Elle est de plus très influencée par les valeurs extrêmes. La médiane se révèle être un meilleur estimateur de la tendance centrale.
Médiane
Au sein d'un échantillon ordonné, c'est la valeur qui sépare un échantillon en deux parties égales. Elle est plus robuste que la moyenne dans le cas de distributions asymétriques ou de valeurs extrêmes, mais elle se prête moins bien aux calculs.
Mesures de dispersion[1]
Variance et écart-type
Au sein d'un échantillon, on calcule les écarts entre les valeurs prises par une variable et la moyenne de cette variable. On calcule la variance qui est la moyenne de ces écarts élevés au carré (afin d’avoir des valeurs positives). La racine carrée de la variance s'appelle l'écart-type. Une petite variance est signe que les valeurs sont proches les unes des autres alors qu'une variance élevée est signe que celles-ci sont très écartées. Ces deux mesures sont sensibles aux valeurs extrêmes.
Intervalle interquartile
Un quartile est chacune des 3 valeurs (Q25, Q50 et Q75) qui divisent les données triées en 4 parts égales. L'intervalle interquartile s'obtient en notant le premier et le troisième quartile. Il est moins sensible aux valeurs extrêmes que la variance et l'écart-type.
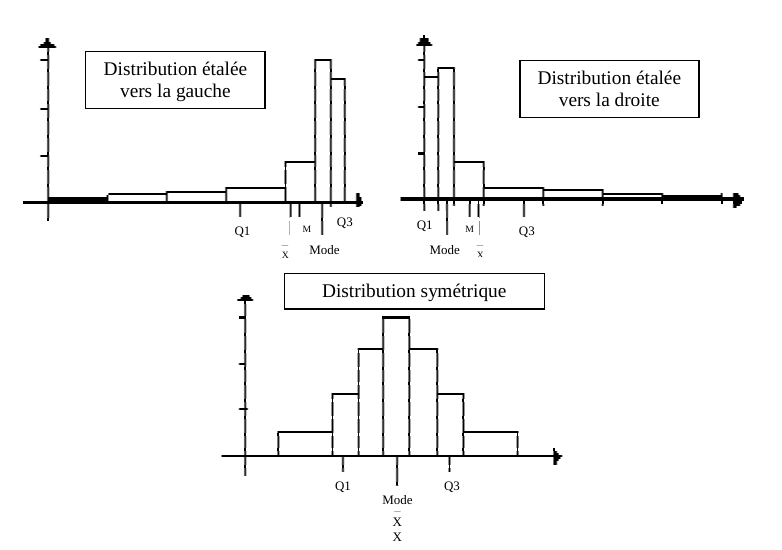
Figure 1. Exemples de distributions statistiques. Les principaux paramètres de position et de dispersion sont reportés.
1. Ancelle T. Statistique Epidémiologie. (2011), Maloine.
Informations professionnelles
- AFMU
- Agenda
- Annonces de postes
- Annuaire de l'urgence
- Audits
- Calculateurs
- Cas cliniques
- Cochrane PEC
- Consensus
- Consensus SFMU
- COVID-19
- DynaMed
- E-learning
- Géodes
- Grand public
- Librairie
- Médecine factuelle
- Outils professionnels
- Portail de l'urgence
- Recherche avancée
- Référentiels SFMU
- Textes réglementaires
- UrgencesDPC
- Webinaire
- Weblettre
Actualites APM
- [30/03/2024] Le CHU d'Angers ouvre une unité d'hospitalisation psychiatrique…
- [30/03/2024] Intérêt d'une intervention aux urgences pour le sevrage tabagique avec…
- [30/03/2024] L'EPSM de la Guadeloupe non certifié par la HAS
- [30/03/2024] Catherine Vautrin au CH de Troyes pour la pose de la première pierre du…
- [Toutes les actualités]
 Rechercher
Rechercher Se connecter
Se connecter Adhérer
Adhérer






 Adhérer à la SFMU
Adhérer à la SFMU Alerte sanitaire
Alerte sanitaire Inscription newsletter
Inscription newsletter