Fluctuation d’échantillonnage et Intervalle de confiance

Luc-Marie JOLY, Julie DUMOUCHEL Commission recherche SFMU 2015

On ne dispose qu'exceptionnellement de l'ensemble des sujets potentiellement incluables dans une étude biomédicale. En réalité, on ne travaille que sur un groupe de sujets ou d’observations formant un échantillon qu'on espère représentatif de la population totale. Cette "population totale" est d'ailleurs souvent une fiction que l'on serait bien incapable de réunir pour l'étudier, voire même de définir précisément dans certains cas. Mesurons une variable chez chacun des sujets de cet échantillon (par exemple la fréquence cardiaque chez les sujets se présentant aujourd'hui dans vos urgences) et calculons la moyenne de ces observations. Il est probable qu'on obtiendrait des valeurs différentes si on avait travaillé sur un autre échantillon (par exemple les sujets se présentant aux urgences de l'hôpital voisin), et donc une moyenne différente. Cependant, ces deux moyennes ne devraient pas trop différer si les deux échantillons sont représentatifs de la même population totale, laquelle pourrait être dans ce cas "les sujets se présentant aux urgences d'un centre hospitalier français". On voit bien qu'on ne pourra jamais réunir pour une étude tous les sujets qui répondent à cette définition et que seul un travail sur échantillon est réalisable. Comme la moyenne mesurée sur un quelconque échantillon a peu de chance d'être identique à la moyenne mesurée sur la population totale, on parle de moyenne estimée. Cette variation de la variable mesurée entre plusieurs échantillons différents de sujets appartenant pourtant à la même population est appelée fluctuation d'échantillonnage [1]

L'exemple pédagogique classique en statistique repose sur une urne contenant par exemple 10 boules noires (BN) et 10 boules blanches (BB): Si vous tirez 10 boules au hasard, vous avez une bonne chance de tirer 5 BN et 5 BB, soit une proportion de 50 % de BN; mais des proportions de 40 ou 60 % de BN, bien qu'un peu moins fréquentes, ne sont pas rares. Quand à ne tirer aucune BN, la probabilité d'un tel événement est non nulle mais très faible. Ces probabilités sont régies par une loi très importante en statistique appelée loi binomiale. Quoiqu'il en soit, si on répète le tirage un grand nombre de fois, la proportion de BN tirée sera en moyenne de 50 %.

On veut maintenant savoir si la moyenne calculée sur un échantillon est proche ou non de la moyenne de la population totale. Il existe pour cela une méthode statistique qui fonctionne si le paramètre a une distribution "normale", c'est-à-dire si la distribution des valeurs du paramètre autour de sa moyenne adopte la forme d'une courbe de Gauss (Fig 1). Pour toute variable mesurée, et si on a des raisons de penser qu'elle adopte bien une distribution normale (la vérification de cette affirmation sortant du champ de cet article), il est possible de calculer un intervalle de confiance (IC) correspondant à deux valeurs encadrant symétriquement la moyenne. On travaille le plus souvent avec un IC à 95 % qui a 95% de chance de contenir la moyenne (inconnue) de la population totale. On peut répéter le même raisonnement avec un pourcentage qui, comme la moyenne, est un paramètre résumant une série de données.

Il existe des formules pour calculer ces IC qui varient selon le type de paramètre :

- Pour la moyenne, la formule est : IC = m±1.96(écart-type) , l'écart type étant la racine carré de la variance, et avec les valeurs de la moyenne et de la variance estimées sur l’échantillon étudié.

- Pour un pourcentage, la formule est : IC = , où p est le pourcentage estimé sur l’échantillon étudié et n le nombre d'observations. Reprenons l'exemple de l'urne en effectuant 40 tirages de 10 boules parmi les 20 : si on obtient en moyenne 52 % de BN, l'IC à 95 % du pourcentage de BN est : = 52 ± 15,5 % = [36,5 % ; 67,5 %]. Cet IC a 95% de chances de contenir le pourcentage vrai de BN, qui dans cet exemple particulier est connu et égal à 50%.

Dans ces formules le nombre 1,96 est le coefficient fixé par la loi normale pour un IC à 95 %. Il est très proche de 2, de telle façon que on peut dire que 95% des observations sont contenues dans l'intervalle de l'IC déterminé par "moyenne +/- 2 écarts-type". On peut noter que la largeur de cet intervalle sera d’autant plus faible, et donc la précision de l’estimation du paramètre d’autant meilleure, que le nombre d'observations est élevé.

La bonne compréhension de ce que signifient les fluctuation d’échantillonnage des paramètres de position que sont la moyenne ou un pourcentage et l'évaluation de leur dispersion par le calcul de leurs IC est essentielle en statistique. Les IC interviendront quand il faudra comparer des échantillons entre eux pour savoir quelle est la probabilité qu'ils soient différents l'un de l'autre.

[1] http://mathematiques.ac-bordeaux.fr/pedalyc/seqdocped/statproba/dia_flu_ech/fluct_echantillonnage.pdf

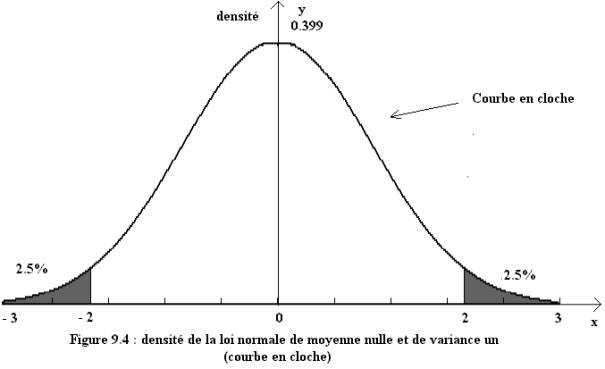
La courbe de gauss est une courbe de densité d'incidence qui regroupe les observations dont la valeur est indiquée sur l'axe des ordonnées. En abscisses, on indique le nombre d'observation pour chaque valeur. La courbe est symétrique et centrée sur la moyenne des observations. L'IC95% est construit par l'intervalle compris entre +/- 2 écarts-type autour de la moyenne et contient 95% des observations. A contrario, seules 2,5% des observations sont situées en dessous de la borne inférieure et 2,5% au-dessus de la borne supérieure. Cet IC95%, visualisé par l'étalement de la courbe, donne une idée de la dispersion des valeurs autour de la moyenne.